Crypto Factzors
First DEFCON – first crypto village CTF! Unfortunately, this was the only puzzle on which I managed to make any progress. I only managed to get as far as I did with the help of some awesome people hanging out in the crypto village. In the end, I couldn’t puzzle out the key… but I did manage to solve the bulk of the puzzle. Thanks, Darío for convincing me to do this write-up!

The prompt of this puzzle reads:
The below phrases have been encrypted using advanced ministry encryption primitives. Decode and report back any hidden messages!
With six encryption “primitives” defined as follows:
enc0 = lambda p: p ^ 0xC7
enc1 = lambda p: ((27 * p) + 33) % 256
enc2 = lambda p: ((7 ** p) * p) % 256
enc3 = lambda p: (
((p & 3) << 2) +
((p & 12) << 4) +
((p & 48) >> 4) +
((p & 192) >> 2)
)
enc4 = lambda p: RIJNDAEL_SBOX[p]
def enc5(p):
if p == 0:
return 0
elif (p % 2) == 0:
return (enc5(p/2) * 6) % 256
else:
return (enc5(p - 1) + 11) % 256
There are six groups of cipher text, which are each apparently lists of decimal encoded bytes, with a terminating semicolon and another trailing number:
030 012 035 030 021 027 036 087 032 016 034 026 028 024 029 030 042 036 045 045 090 043 035 051 063 054 050 040; 361083 205 003 003 071 030 111 044 017 107 098 071 151 017 179 232 057 031 017 206 206 112; 85088 107 190 097 097 243 113 194 220 024 167 165 206 112 236 112 120; 1007101 161 105 109 236 152 097 169 034 042 097 037 101 025 042 169 085 170 166 230 226 234; 1829138 234 221 198 068 120 116 181 037 112 189 189 180 112 014 095 232 185 053 087 139 097 139 217; 341227 037 026 111 089 150 095 111 211 089 131 023 023 002 161 211 211 095 084 186; 21
The final clue is the text at the bottom:
It appears the ministry is employing some kind of anti-analysis countermeasures! The below obfuscated clue may prove useful:
And the following obfuscated python code:
hint = lambda p,k: ''.join(chr((ord(x)+k)%256) for x in p)
exec(hint('_\x88}\x8c\x93\x8a\x8e:W:\x86{\x87|~{:yFyyFyyyT:uyBByyu\x83wEyyyE\x83C?LOPC:\x80\x89\x8c:\x83:\x83\x88:\x8c{\x88\x81\x7fB\x86\x7f\x88ByyCCw',0xe6))
I evaluated the first line in the python3 interpreter to define the hint
function, then evaluated only the argument to the exec call – just to
see what hint outputs. It turns out to be the text of a lambda
expression:
Encrypt = lambda _,__,___: [_((__[i]+___+i)%256) for i in range(len(__))]
Based on the name of the variable the lambda expression is stored in, this appears to be the function with which the above cipher text was generated! Score!
The first argument to the expression appears to be a callable, the
second argument a sequence, and the third an integer. So, the Encrypt
function appears to take some cipher function, the clear text to encrypt
(as a bytes object or as an array of integers), and a key.
Clearly, to decipher the messages, I need to reverse not only the
Encrypt function, but also each of the given cryptographic primitives –
which I assume are the callables supplied as the first argument to the
function.
I started with the easiest one: the symmetric enc0. Because the
exclusive or operation is symmetric (e.g. (a ^ b) ^ b == a),
dec0 = enc0.
Then, I tried to puzzle through enc1… and got nowhere. A very smart
person sat down next to me in the village and taught me about rings and
fields – and we eventually found the Wikipedia page on the
Modular Multiplicative Inverse.
We decided to try to use Euler’s theorem, which defines the modular
inverse as a ** (φ(m) - 1), where φ is Euler’s totient function, a
is the coefficient we’re trying to invert, and m is the size of the
ring. According to the wiki, this holds only if a and m are co-prime
(sharing no common factor except 1). Again, according to
the wiki:
Euler’s totient function counts the positive integers up to a given integer n that are relatively prime to n.
Because our n is 256 (a power of 2), only even numbers share any factors
with it. So, φ(256) = (256 / 2) - 1 – or the number of odd numbers
between 1 and 256. Great, so our multiplicative inverse is
(27 ** 127) % 256 == 19, and the inverse of enc1 is
dec1 = lambda p: ((p - 33) * 19) % 256
Given how hard (for me) the second function was to reverse, I decided to
try something more in my wheelhouse: shuffling bits! enc3 shuffles the
bits of the input byte according to the following diagram:
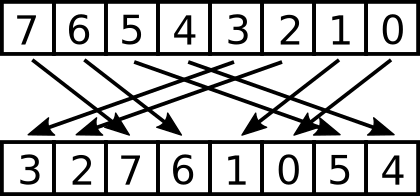
The inverse is simple to derive:
dec3 = lambda p: (
((p & 3) << 4) +
((p & 12) >> 2) +
((p & 48) << 2) +
((p & 192) >> 4)
)
enc4 is simple as well, as the Rijndael S-boxes are well known. See the
Wikipedia article.
dec4 = lambda p: invRijndael[p]
Now we’ve run out of easy work to do, and I didn’t want to get into learning about discrete logarithms, so I applied the first principal virtue of programmers: laziness! That same smart person that taught me about rings pointed out that the space we’re searching is tiny, and that these hard problems can be reversed with a lookup table. Therefore:
dec2_table = [enc2(x) for x in range(256)]
dec2 = lambda p: dec2_table[p]
dec3_table = [enc3(x) for x in range(256)]
dec3 = lambda p: dec3_table[p]
Next, reversing the Encrypt function gave me a bit of trouble. It took
an embarrassing amount of time for me to realize that the operations not
only had to be inverted (e.g. addition becomes subtraction), but also that
they had to be applied in reverse order!
Decrypt = lambda a, b, c: [
((a(b[i]) - c - i) % 256) for i in range(len(b))
]
I reasoned that the trailing number after the cipher text is meant for
the third argument, so I tried bytes(Decrypt(dec0, cipher1, key1))
because the output of Decrypt is actually just a list of ints, and not
immediately readable to me. To my delight, out pops:
b'payment verification network'
Success! I decrypted the other cipher text in exactly the same way, using the next decryption primitive for each. All the deciphered messages are below:
b'payment verification network'
b'anonymous transactions'
b'immutable history'
b'proof instead of trust'
b'zero-government currency'
b'decentralized ledger'
Unfortunately, this is where I got stuck. I’m no good at crossword
puzzles, and these messages read very much like the hints to one of
those… I tried the obvious words and phrases for the flag, such as
cryptocurrency, bitcoin, monero, and blockchain to no avail. The
prompt text says to report any hidden messages, so I tried concatenating
the first letter of every message, and of every word, etc… Nada.
I never got the chance to ask anyone in the village who had already solved it, so this one will remain a mystery.
I hope I’ll have better luck next year!